Mandala version 0.4, web page version 0.4.2.
This page best viewed in a medium-skinny window.
Here, besides the applet, you will find
In short, it's rotation transformations, modified in a reversible way for integers. The color of each point is based on how many applications of a rotation are required to get back to that same point.
I was writing a lossless audio compression program. Compression
puts 16-bit integers through one transformation; there has to be
an opposite "expansion" transformation that restores the
exact original integers, in order for the process to be lossless.
The method I was trying involves the fast Fourier transform (FFT),
which takes pairs of values and treats them like
( x, y ) coordinates of points to be rotated around the origin
of a coordinate space.

This operation is also used to rotate pictures in graphics software. Rotations around the origin can be done by representing the point as a vector of two elements, and multiplying by a 2 x 2 matrix like this:
| cos theta -sin theta |
p | | = q
| sin theta cos theta |
where p is the original point, theta is the angle, and q is the new
point. This trick is called a "Givens rotation" sometimes. The
matrix multiplication above is equivalent to these calculations:
new x = old x * cos( theta ) - old y * sin( theta )
new y = old x * sin( theta ) + old y * cos( theta )
If you are working in integers, or fixed point--or in floating point for
that matter--there's a grid of points you can represent exactly, and
points that start on the grid don't always end up on the grid after
being rotated. So, which grid point do you choose?
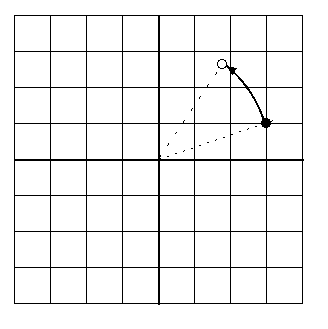
In applications like lossless compression, some rounding error is okay as long as the rotation is reversible so that the original data can be reconstructed from the data that went through the transformation. This is the same as requiring that no two points transform to the same point.
There is a technique called "lifting" that makes the rotation reversible by "factoring" the Givens rotation matrix into a product of three matrices, so that the rotation turns into this multiplication:
| 1 0 | | 1 sin theta | | 1 0 |
| | | | | |
p | (cos theta) - 1 | | | | (cos theta) - 1 | = q
| --------------- 1 | | | | --------------- 1 |
| sin theta | | 0 1 | | sin theta |
That's two more matrix multiplications, but actually about the same amount of calculating. To do it exactly, calculating q = ( x2, y2 ) from p = ( x0, y0 ), would go like this:
x1 = x0 + y0 * ( cos( theta ) - 1 ) / sin( theta ) y2 = y0 + x1 * sin( theta ) x2 = x1 + y2 * ( cos( theta ) - 1 ) / sin( theta )(Here you can actually change x and y in place, but I gave them subscripts to give names to the different states.)
The integer approximation to the same thing goes like this:
x1 = x0 + round( y0 * ( cos(theta) - 1 ) / sin(theta) ) y2 = y0 + round( x1 * sin(theta) ) x2 = x1 + round( y2 * ( cos(theta) - 1 ) / sin(theta) )(where the round() function finds the nearest integer).
The reason the calculation is reversible, even though the rounding causes errors, is this: on each of the three lines above, the expression that's being rounded is calculated from a variable that isn't changing in that line, and added to another variable. To reverse the calculation, just reverse the order of the lines and subtract what was added:
x1 = x2 - round( y2 * ( cos(theta) - 1 ) / sin(theta) ) y0 = y2 - round( x1 * sin(theta) ) x0 = x1 - round( y0 * ( cos(theta) - 1 ) / sin(theta) )
Since the exact same expressions are being calculated and rounded, the exact original values can be reconstructed.
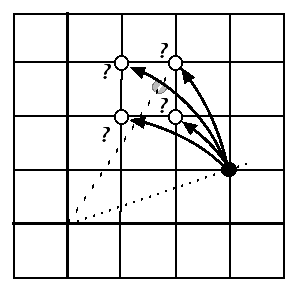
Here's a picture
of a grid of points being put through these three transformations.
Each of the steps skews the picture. On the left the
calculations are exact; on the right, rounded.

As you can see, the points in the integer-math version are approximately where they should be, but they've wandered in various directons, making the grid wrinkly. Thinking about this got me very curious and I wrote a program to produce some of the visualizations on this page.
For instance, I wondered: suppose the rotation angle is an even fraction of 360 degrees,
say 1/8.
Start
with a point and do an integer-approximated 45 degree rotation--
eight times. Where do we end up...back at the original point?
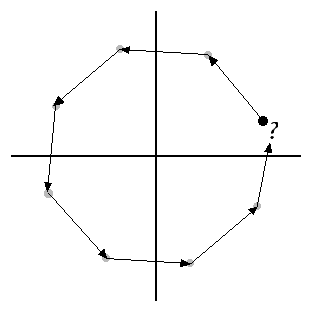
Well, sometimes. Here's a grid after eight 45 degree rotations:

Many of the points seem to have returned to their original places. Others seem to be moving in swirls of some kind, although it's not too clear from this picture. Wanting a better visualization of this led to the Mandala program. Mandala lets you set the numerator and denominator of a fraction of 360 degrees. Then, when you click the "Draw" button, it goes through each point on a grid and counts how many transformations by that angle the point has to be taken through before it gets back to the same place. Then it colors the point --and any other points in the same cycle--based on the length of the cycle. I'm still pretty amazed at the results.
The basic skew operation on an integer grid produces offsets that
are integer multiples of the (usually irrational) slope of the skew,
rounded to integers. If you
look at the difference between successive offsets, there's a
pattern. For instance, if the slope is 1.0, the pattern is
very simple:
| Offset | After rounding | Difference |
|---|---|---|
| 0 | 0 | - |
| 1 | 1 | 1 |
| 2 | 2 | 1 |
| 3 | 3 | 1 |
| 4 | 4 | 1 |
| etc. |
For any slope that's a rational number, the pattern repeats in the same
number of steps as the denominator of the (reduced) fraction. For instance, here's the
pattern for 3/5:
| Offset | After rounding | Difference |
|---|---|---|
| 0 | 0 | - |
| 3/5 | 1 | 1 |
| 6/5 | 1 | 0 |
| 9/5 | 2 | 1 |
| 12/5 | 2 | 0 |
| 15/5 | 3 | 1 |
| 18/5 | 4 | 1 |
| 21/5 | 4 | 0 |
| 24/5 | 5 | 1 |
| 27/5 | 5 | 0 |
| 30/5 | 6 | 1 |
| etc. |
For irrational numbers (like most of the sines and cosines of angles used in this
program) there is a regular pattern, with exceptions occurring at a larger
interval, with exceptions to that pattern occurring at a larger interval, etc.
For instance, for sqrt(2)/2:
| Offset | After rounding | Difference |
|---|---|---|
| 0 | 0 | - |
| .707 | 1 | 1 |
| 1.414 | 1 | 0 |
| 2.121 | 2 | 1 |
| 2.828 | 3 | 1 |
| 3.536 | 4 | 1 |
| 4.243 | 4 | 0 |
| 4.950 | 5 | 1 |
| 5.657 | 6 | 1 |
| 6.364 | 6 | 0 |
| 7.071 | 7 | 1 |
| etc. |
Here the pattern is:
...10111011011011101101110110111011011011101101110......which can be grouped:
...10 1110 110 110 1110 110 1110 110 1110 110 110 1110 110 1110......which can be grouped:
...10 1110 110 110 1110 110 1110 110 1110 110 110 1110 110 1110......and so forth.
The interruptions to the pattern at longer and longer scales roughly correspond to further and further digits of the slope number. In any case, they form a semi-regular fractal pattern of "fault lines" in the skew operation. Looking at a single point in its trip around the origin, it's as if three skew patterns, each rotated through all the multiples of the basic angle, are all overlaid on the grid. The points are like ants going for walks and being nudged one way or another at each step by this kaleidoscopic fractal fault-line pattern. The small-scale patterns in the skew functions result in repeated small walking patterns for the ants; the larger scale patterns of interruptions produce larger round trips for the ants (often composed of pieces of the smaller patterns), and so forth.
These fractal patterns may be related to Penrose tilings (see especially 1/10 Minsky) and/or snowflake crystals (regular crystals forced by the crystal seed into irrational skews?). I haven't figured out why certain denominators produce patterns with no real regularity that I can see. It may be that the regularities are there but only visible at a much larger scale.
Another question I have is this: given an arbitrary rotation approximation of this kind, are all points on cycles, or are there paths that go out to infinity in both directions? If there are infinite paths, under what conditions? If the paths stayed within a certain distance from the origin, you can see that they would have to cycle. But I've seen paths in Mandala that waver over a pretty wide band...
The program can be run as an application instead of an applet. To run the jar file, on some operating systems (e.g. Mac OS X) you can just double-click it. On others, when Java is installed the right way and you're in the right directory, you type this at a command prompt:
java -jar Mandala.jar
Here are a couple pictures of the program in the process of drawing.

Here's a detail from "Please don't nuke Iran,"
which is also the basis of the background of this page.
It's from a Postscript version of the program,
with the fraction set to 1/12.
1024x820 version

Here are some examples of the program run with the Minsky variation and the fraction set at 1/10, which generates what looks like a pentagonal quasicrystal pattern.
-- Steve Witham <sw@not_this.tiac.net>
